1. Hàm số liên tục là gì?
Hàm số y = f(x) gọi là hàm số liên tục trên khoảng nếu hàm số đó liên tục tại mọi điểm thuộc khoảng đó. Cụ thể hơn, ta có định nghĩa khái quát chung như sau:
Cho hàm số y = f(x) xác định trên $K,x_{0}in K$. Khi đó, y = f(x) liên tục tại $x_{0}$ khi $underset{xrightarrow x_{0}}{lim} f(x)=f(x_{0})$.
Đồ thị hàm số liên tục có dạng:
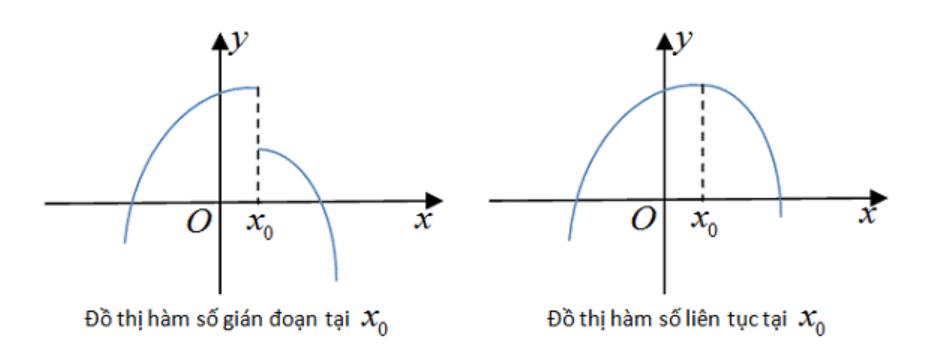
2. Hàm số liên tục tại 1 điểm
Cho hàm số y = f(x) xác định trên (a;b) và $x_{0} epsilon (a;b)$. Hàm số y được gọi là hàm số liên tục tại 1 điểm $x_{0}$ khi $underset{xrightarrow x_{0}}{lim}f(x)=f(x_{0})$.
Ngược lại, nếu hàm số $f(x_{0})$ không liên tục tại $x_{0}$ thì khi đó $x_{0}$ gọi là điểm gián đoạn của f(x).
Nâng cao hơn, nếu ta có 2 hàm số y = f(x) và y = g(x) cùng liên tục tại điểm $x_{0}$. Khi đó:
-
$y=f(x) + g(x) . y = f(x) - g(x) . y=f(x) . g(x)$ sẽ liên tục tại điểm $x_{0}$.
-
$y=frac{f(x)}{g(x)}$ là hàm số liên tục tại $x_{0}$ khi $g(x_{0}) neq 0$.
3. Hàm số liên tục trên một khoảng
Nếu hàm số y = f(x) liên tục trên một khoảng (a;b) thì khi đó hàm số f(x) sẽ liên tục tại mọi điểm thuộc (a;b). Đồ thị hàm liên tục trên khoảng (a;b) được biểu diễn bằng một đường nét liền, không bị đứt gãy.
Các hàm số căn thức, phân thức, hàm số lượng giác đều liên tục trên từng khoảng xác định của chúng.
Ngoài ra, nếu đồ thị hàm số y = f(x) liên tục trên khoảng (a; b) và thỏa mãn $ underset{xrightarrow a^{+}}{lim}f(x)=f(a); underset{xrightarrow b^{-}}{lim}f(x)=f(b)$ thì đồ thị y = f(x) liên tục trên đoạn [a;b].
4. Hàm số liên tục trên r
Hàm liên tục trên R là trường hợp đặc biệt của hàm số liên tục trên một khoảng.
Đối với một số hàm đa thức thì sẽ liên tục trên tập R mà không cần chứng minh, bao gồm: hàm lượng giác y = sinx, y = cosx, hàm đa thức, hàm phân thức có tập xác định R, hàm mũ.
Tham khảo ngay tài liệu tổng hợp kiến thức và phương pháp giải mọi dạng bài tập độc quyền của VUIHOC ngay

5. Một số định lý cơ bản về hàm số liên tục
Để áp dụng giải các bài tập liên quan đến hàm số liên tục, ngoài định nghĩa các loại hàm số liên tục, học sinh cần nắm chắc 3 định lý cơ bản sau đây:
Định lý 1:
-
Hàm số đa thức là loại hàm số liên tục trên tập R.
-
Hàm số thương của 2 đa thức (phân thức hữu tỉ) và các hàm số lượng giác đều liên tục trên từng khoảng của tập xác định.
Định lý 2: Cho hàm số y = f(x) và y = g(x) là hai hàm số liên tục tại $x_{0}$.
Ta có:
-
$y=f(x) + g(x) . y=f(x) - g(x),y=f(x) . g(x)$ sẽ liên tục tại điểm $x_{0}$.
-
$y=frac{f(x)}{g(x)}$ là hàm số liên tục tại $x_{0}$ khi $g(x_{0}) neq 0$.
Định lý 3: Cho hàm số y = f(x) liên tục trên [a;b] và thỏa mãn f(a) . f(b) < 0. Tồn tại ít nhất 1 điểm c thuộc đoạn (a;b) thỏa mãn f(c) = 0.
Định lý này thường dùng để chứng minh sự tồn tại nghiệm của phương trình trên khoảng nhất định.
Định lý 3 còn có một dạng khác như sau:
Cho hàm số y = f(x) liên tục trên [a;b] và thỏa mãn f(a) . f(b) < 0. Phương trình f(x) = 0 sẽ có ít nhất 1 nghiệm trong khoảng (a;b).
6. Các dạng bài tập về hàm số liên tục và ví dụ cụ thể
6.1. Dạng 1: Xét tính liên tục của hàm số tại một điểm
Đây là dạng bài thường gặp trong chuyên đề hàm số liên tục. Để xét tính liên tục của hàm số tại 1 điểm, ta tiến hành theo các bước sau:
Bước 1: Tính giá trị $f(x_{0})$
Bước 2: Tính giá trị $underset{xrightarrow x_{0}}{lim}f(x)$ hoặc $underset{xrightarrow x_{0}^{+}}{lim}f(x), underset{xrightarrow x_{0}^{-}}{lim}f(x)$
Bước 3: So sánh hai giá trị $underset{xrightarrow x_{0}}{lim}f(x)$ hoặc $underset{xrightarrow x_{0}^{+}}{lim}f(x), underset{xrightarrow x_{0}^{-}}{lim}f(x)$ với $f(x_{0})$ đã tính ở bước 1, rồi kết luận.
-
Nếu giá trị $underset{xrightarrow x_{0}}{lim}f(x)=f(x_{0})$ hoặc $underset{xrightarrow x_{0}^{+}}{lim}f(x),underset{xrightarrow x_{0}^{-}}{lim}f(x)=f(x_{0})$ thì học sinh kết luận hàm số f(x) liên tục tại điểm $x_{0}$.
-
Nếu giá trị $underset{xrightarrow x_{0}}{lim}f(x)$ không tồn tại hoặc $underset{xrightarrow x_{0}}{lim}f(x) neq 0$ thì học sinh kết luận hàm số f(x) không liên tục tại điểm $x_{0}$.
Bước 4: Kết luận dựa theo yêu cầu đề bài.
Ví dụ 1: Xét tính liên tục tại x = 1 của hàm số sau đây:
$left{begin{matrix} frac{2 - 7x + 5x^{2}}{x^{2} - 3x +2} & khi , x neq 1 -3 & khi , x = 1 end{matrix}right.$
Giải:
Hàm số đề bài xác định trên R{2} có x = 1 và f(1) = -3
Tính giới hạn hàm số tại điểm x = 1:
$underset{xrightarrow 1}{lim}f(x)=underset{xrightarrow 1}{lim} frac{2 - 7x + 5x^{2}}{x^{2} - 3x + 2}=underset{xrightarrow 1}{lim} frac{(x - 1)(5x - 2)}{(x - 1)(x - 2)}=underset{xrightarrow 1}{lim} frac{5x - 2}{x - 2}=-3$
Ta thấy: $underset{xrightarrow 1}{lim}f(x)=f(1)=-3$. Suy ra hàm số đề bài liên tục tại $x_{0}=1$
Ví dụ 2: Xét tính liên tục của hàm số sau đây tại điểm x = 1:
Giải:
Hàm số đề bài cho xác định tại x = 1 và f(1) = 1
Tính giới hạn trái tại x = 1:
$underset{xrightarrow 1^{-}}{lim}f(x)=underset{xrightarrow 1^{-}}{lim}1=1$
Tính giới hạn phải tại x = 1:
$underset{xrightarrow 1^{+}}{lim}f(x)=underset{xrightarrow 1^{+}}{lim} frac{2 - 7x +5x^{2}}{x^{2} - 3x + 2}=underset{xrightarrow 1^{+}}{lim} frac{5x - 2}{x - 2}=-3$
Vì $underset{xrightarrow 1^{+}}{lim}f(x) neq underset{xrightarrow 1^{-}}{lim}f(x)$ nên hàm số gián đoạn tại x = 1.
6.2. Dạng 2: Xét tính liên tục, chứng minh hàm số liên tục trên một khoảng đoạn hoặc tập xác định
Đối với dạng bài tập này, học sinh cần áp dụng phối hợp 2 định lý 1 và 2 để xét tính liên tục của hàm số đề bài trên từng khoảng xác định của nó. Nếu hàm số đã cho xác định, các em học sinh tiếp tục xét tính liên tục tại các điểm đặc biệt của hàm số đó.
Ví dụ 1: Chứng minh hàm số sau đây liên tục trên khoảng (-7;+)
$f(x)=left{begin{matrix} x^{2} - x + 4, x geq 2 frac{x - 2}{sqrt{x + 7 - 3}}, -7 < x < 2 end{matrix}right.$
Giải:

Ví dụ 2: Tìm giá trị a, b sao cho hàm số sau liên tục:
$left{begin{matrix} 1, x < 3 ax + b, 3 leq x leq 5 3, x > 5 end{matrix}right.$
Giải:

6.3. Dạng 3: Tìm điều kiện hàm số liên tục tại 1 điểm
Đây là dạng toán “tìm m” rất phổ biến trong các đề luyện thi và các đề kiểm tra trong chương trình học phổ thông. Phương pháp giải dạng toán này gồm có 3 bước:
Bước 1: Tìm điểm xác định $x_{0}$ của hàm số đề bài. Tính giá trị f(m) với $m = x_{0}$
Bước 2: Tính giới hạn của hàm số đề bài tại $x_{0}$
Bước 3: Hàm số f(x) liên tục tại $x_{0}$ khi và chỉ khi $underset{xrightarrow x_{0}}{lim}=f(x_{0})$
Bước 4: Kết luận giá trị của m.
Các em cùng xét ví dụ sau đây:
Ví dụ 1: Tìm giá trị m để hàm số sau liên tục tại điểm x = 1
Giải:
Ta xét hàm số xác định tại x = 1 và f(x) = -3m . 1 - 1.
Tính giới hạn hàm số tại điểm x = 1
$underset{xrightarrow 1}{lim} f(x) = underset{xrightarrow 1}{lim} frac{2 - 7x + 5x^{2}}{x^{2} - 3x + 2} = underset{xrightarrow 1}{lim} frac{(x -1)(5x - 2)}{(x - 1)(x - 2)}=underset{xrightarrow 1}{lim} frac{5x - 2}{x - 2}=-3$
Vậy, hàm số f(x) liên tục tại điểm $x_{0}=1$ khi:
$underset{xrightarrow 1}{lim}f(x)=f(1) Leftrightarrow -3m -1 Leftrightarrow m=-frac{2}{3}$
Kết luận: $m=frac{-2}{3}$
Ví dụ 2:
Giải:
Ta có $underset{xrightarrow -2^{-}}{lim}f(x)=underset{xrightarrow -2^{+}}{lim}f(-2) Leftrightarrow -2a - 1 = -11 Leftrightarrow a=5$
Vậy giá trị a cần tìm là 5.
Đăng ký ngay để được các thầy cô xây dựng lộ trình và ôn tập kiến thức đạt 9+ ôn thi tốt nghiệp THPT

6.4. Dạng 4: Tìm điều kiện để hàm số liên tục trên một khoảng đoạn hoặc tập xác định
Đối với các bài toán tìm điều kiện để hàm số liên tục trên một đoạn hoặc một tập xác định bất kỳ, học sinh làm tương tự dạng 3. Điểm khác biệt duy nhất là ở dạng 3 ta tìm điểm làm hàm số xác định, còn với dạng này ta tìm khoảng đoạn hoặc tập làm cho hàm số xác định.
Xét bài toán ví dụ sau đây:
Ví dụ 1: Tìm giá trị m để hàm số sau đây liên tục trên tập xác định:

Giải:
Tập xác định của hàm số là R
Xét trường hợp $x neq 1$, hàm số có dạng $f(x)=frac{2 - 7x + 5x^{2}}{x-1}$. f(x) là hàm phân thức hữu tỉ nên tập xác định là $(-infty; 1) cup (1; +infty)$ vì vậy f(x) cũng liên tục trên khoảng $(-infty; 1) cup (1; +infty)$
Xét trường hợp x = 1 thì ta có f(1) = -3m - 1:
$underset{xrightarrow 1}{lim}f(x)=underset{xrightarrow 1}{lim} frac{2 - 7x +5x^{2}}{x-1}=underset{xrightarrow 1}{lim} frac{(x-1)(5x - 2)}{x - 1}=3$
Khi đó, hàm f(x) liên tục tại điểm $x_{0} = 1$ khi và chỉ khi:
$underset{xrightarrow 1}{lim}f(x)=f(1) Leftrightarrow 3m - 1=3 Leftrightarrow m=-frac{4}{3}$
Kết luận: $m=-frac{4}{3}$
Ví dụ 2: Tìm m để hàm số sau đây liên tục trên $[0;+infty)$
$left{begin{matrix} frac{3-sqrt{9-x}}{x}, & 0 < x < 9 m,& x=0 frac{1}{18m},&xgeq 9 end{matrix}right.$
Giải:

6.5. Dạng 5: Ứng dụng tính liên tục của hàm số để chứng minh phương trình có nghiệm
Ta cùng xét các ví dụ sau đây để hiểu về cách ứng dụng tính liên tục của hàm số chứng minh phương trình có nghiệm:
Ví dụ 1: Chứng minh rằng phương trình $3x^{3} + 2x - 2 = 0$ có nghiệm trong (0; 1).
Giải:
Hàm số đề bài là hàm đa thức, cho nên f(x) liên tục trên R. Suy ra, f(x) cũng liên tục trên đoạn [0;1].
Ta có:
f(0) . f(1) = (-2) . (3) = -6 < 0
Do vậy, có ít nhất 1 số c trong (0; 1) sao cho f(c) = 0. Hay nói cách khác, phương trình f(x) = 0 có ít nhất 1 nghiệm thuộc (0; 1).
Ví dụ 2: Chứng minh rằng, phương trình $2x^{3} - 6x^{2} + 5 = 0$ trong khoảng (-1;3) có 3 nghiệm phân biệt.
Hàm số đề bài liên tục trên R, do đó f(x) liên tục trên các đoạn [-1;0], [0;2], [2;3].
Ta thấy: f(-1) = -3, f(0) = 5, f(2) = -3, f(3) = 5. Từ đó:
f(-1) . f(0) < 0
f(0) . f(2) < 0
f(2) . f(3) < 0
Vì vậy, phương trình đề bài có nghiệm trong các khoảng (-1;0),(0;2) và (2;3).
Từ đó ta có thể kết luận phương trình có 3 nghiệm phân biệt trong khoảng (-1; 3).
6.6. Dạng 6: Sử dụng tính liên tục để xét dấu hàm số
Khi xét dấu hàm số có áp dụng tính liên tục của hàm số, học sinh cần sử dụng kết quả: “Nếu hàm số y = f(x) là hàm liên tục và không triệt tiêu trên [a;b] thì khi đó có dấu nhất định trên (a;b)”
Xét các ví dụ sau:
Ví dụ: Xét dấu của hàm số sau: $f(x)= sqrt{x+4} - sqrt{1-x} - sqrt{1-2x}$
Giải:
7. Một số bài tập về hàm số liên tục từ cơ bản đến nâng cao và phương pháp giải
Để thành thạo các dạng bài tập hàm số liên tục, các em học sinh cùng vuihoc giải các bài tập luyện tập sau đây!
Bài 1: Xét tính liên tục của hàm số sau tại điểm x = 0
Giải:
Hàm số đề bài xác định tại x = 0 và f(0) = 2
Xét giới hạn trái tại điểm x = 0:
$underset{xrightarrow 0^{-}}{lim} f(x)=underset{xrightarrow 0^{-}}{lim} (2x + frac{1}{4})=frac{1}{4}$
Xét giới hạn phải tại x=0:
$underset{xrightarrow 0^{+}}{lim} f(x)=underset{xrightarrow 0^{+}}{lim} frac{sqrt{x + 4}-2}{x}=underset{xrightarrow 0^{+}}{lim}frac{sqrt{x + 4}-2}{(sqrt{x+4})^{2}-4}=underset{xrightarrow 0^{+}}{lim}frac{1}{sqrt{x+4} + 2}=$
Xét thấy, $underset{xrightarrow 0^{+}}{lim} f(x)=underset{xrightarrow 0^{-}}{lim} f(x)$ nhưng lại khác f(0). Do đó, hàm số không liên tục tại x=0
Bài 2: Xét tính liên tục trên R của hàm số sau:

Giải:
Trường hợp x < 0: f(x) = 2x - 1 là hàm số liên tục
Trường hợp x > 0: $f(x) = sqrt{x}$ là hàm số liên tục
Từ đó suy ra, ta chỉ xét tính liên tục của hàm số tại x = 0 là có thể kết luận tính liên tục của hàm số đề bài.
$underset{xrightarrow 0^{+}}{lim} f(x)=underset{xrightarrow 0^{+}}{lim} sqrt{x}=0$
$underset{xrightarrow 0^{-}}{lim} f(x)=underset{xrightarrow 0^{-}}{lim} (2x - 1)= -1$
Xét thấy $underset{xrightarrow 0^{+}}{lim} f(x)=f(0) neq underset{xrightarrow 0^{-}}{lim} f(x)$. Do đó, hàm số gián đoạn tại điểm x = 0.
Kết luận: hàm số không liên tục trên tập xác định.
Bài 3: Chứng minh phương trình $ax^{2} + bx + c = 0$ luôn tồn tại nghiệm trong $[0; frac{1}{3}]$ với mọi $a neq 0$ và thỏa mãn điều kiện 2a + 6b + 19c = 0
Giải:
Bài 4: Tìm giá trị a để hàm số sau đây liên tục tại x = 2

Giải:
Bài 5: Hàm số f(x) sau đây liên tục trên R khi nào?
$y = f(x) = left{begin{matrix} 2x + 3 & khi , xgeq 1 m + 2 & khi , x < 1 end{matrix}right.$
Giải:
Dễ thấy hàm số đã cho liên tục với mọi x khác 1
Vì vậy để hàm số liên tục trên $mathbb{R}$ thì $underset{xrightarrow 1^{+}}{lim} f(x) = underset{xrightarrow 1^{-}}{lim} f(x) = f(1) Leftrightarrow 5 = m + 2 Leftrightarrow m=3$
Vậy với m = 3 thì hàm số đã cho liên tục trên $mathbb{R}$
Bài viết trên đây đã tổng hợp toàn bộ lý thuyết và các dạng bài tập cơ bản của hàm số liên tục trong chương trình toán lớp 11. Hy vọng rằng sau bài viết này, các em học sinh sẽ nắm vững định nghĩa và các định lý để áp dụng làm bài tập. Để học thêm nhiều kiến thức Toán THPT bổ ích, các em đừng quên truy cập Vuihoc.vn hoặc liên hệ trung tâm hỗ trợ để mở ra cánh cổng tri thức chinh phục kỳ thi THPT Quốc gia sắp tới nhé!
Bài viết có thể tham khảo thêm:
Giới hạn của dãy số
Giới hạn của hàm số
Định nghĩa và ý nghĩa của đạo hàm


